在市區過馬路,是日常生活的一部分,平日倒是習以為常的,也很少會想起什麽。若是要運貨之類的,市區的路也早已規劃好了,沿着路走就行。
若是一些郊外的地方,要把貨物由貨倉運去一個指定的地方,比如河的對岸,那麽途中河上那道橋的位置,就會很影響運輸的效率,這裡有個規劃的問題。
為了簡化問題,不妨設兩邊河岸是互相平行的。而造橋時為了節省材料,不妨假設橋都是垂直於河岸的,那樣就是兩邊河岸的最短距離(圖一)。
問 題
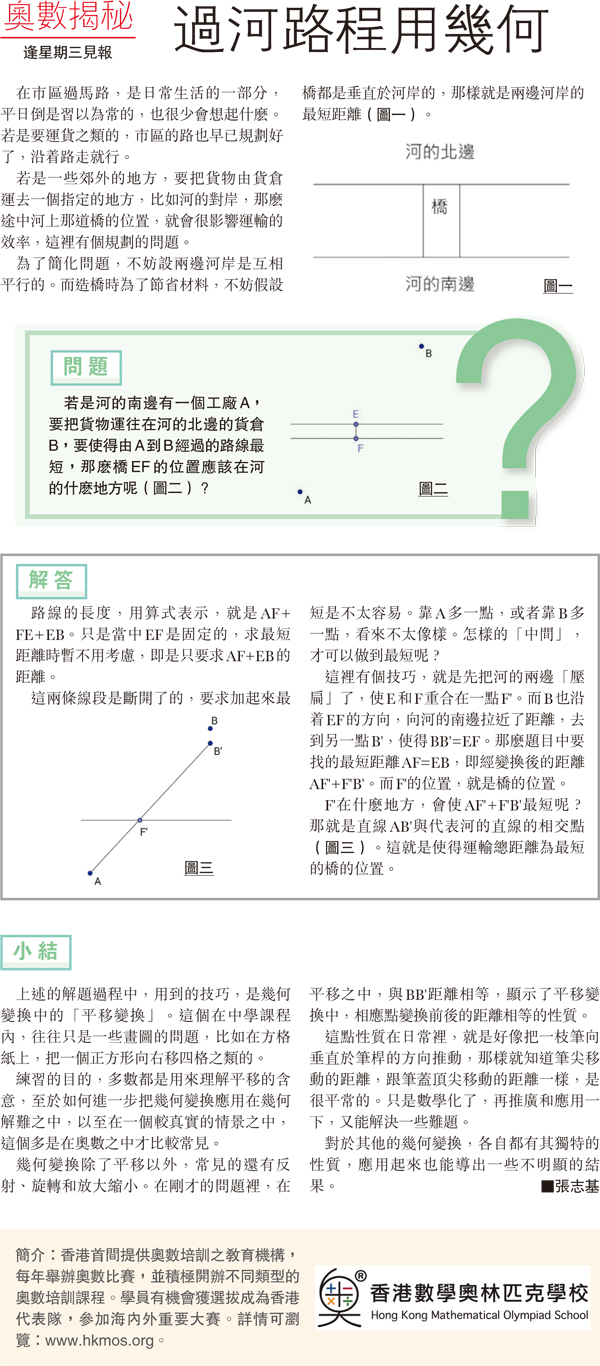
若是河的南邊有一個工廠A,要把貨物運往在河的北邊的貨倉B,要使得由A到B經過的路線最短,那麽橋EF的位置應該在河的什麽地方呢(圖二)?
解 答
路線的長度,用算式表示,就是AF+FE+EB。只是當中EF是固定的,求最短距離時暫不用考慮,即是只要求AF+EB的距離。
這兩條線段是斷開了的,要求加起來最短是不太容易。靠A多一點,或者靠B多一點,看來不太像樣。怎樣的「中間」,才可以做到最短呢?
這裡有個技巧,就是先把河的兩邊「壓扁」了,使E和F重合在一點F'。而B也沿着EF的方向,向河的南邊拉近了距離,去到另一點B',使得BB'=EF。那麽題目中要找的最短距離AF=EB,即經變換後的距離AF'+F'B'。而F'的位置,就是橋的位置。
F'在什麽地方,會使AF'+F'B'最短呢?那就是直線AB'與代表河的直線的相交點(圖三)。這就是使得運輸總距離為最短的橋的位置。
小 結
上述的解題過程中,用到的技巧,是幾何變換中的「平移變換」。這個在中學課程內,往往只是一些畫圖的問題,比如在方格紙上,把一個正方形向右移四格之類的。
練習的目的,多數都是用來理解平移的含意,至於如何進一步把幾何變換應用在幾何解難之中,以至在一個較真實的情景之中,這個多是在奧數之中才比較常見。
幾何變換除了平移以外,常見的還有反射、旋轉和放大縮小。在剛才的問題裡,在平移之中,與BB'距離相等,顯示了平移變換中,相應點變換前後的距離相等的性質。
這點性質在日常裡,就是好像把一枝筆向垂直於筆桿的方向推動,那樣就知道筆尖移動的距離,跟筆蓋頂尖移動的距離一樣,是很平常的。只是數學化了,再推廣和應用一下,又能解決一些難題。
對於其他的幾何變換,各自都有其獨特的性質,應用起來也能導出一些不明顯的結果。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

