這次介紹一道幾何題,順道談談怎樣善用課程內的數學打穩奧數的基礎。
問 題:在平行四邊形ABCD中,P和Q分別是BC和CD上的兩點,且S△BAP = S△DAQ,求證PQ // BD。
答 案:考慮△BAP和△BDP,以BP為底的話,兩者等高,因此S△BAP = S△BDP。
再考慮△DAP和△DBQ,以DQ為底的話,兩者等高,因此S△DAQ = S△DBQ。
由條件S△BAP = S△DAQ得知,S△BDP = S△DBQ,若以BD為底,則兩高相等,即P和Q與直線BD距離相等,由於P和Q都在BD的下方,因此PQ // BD。
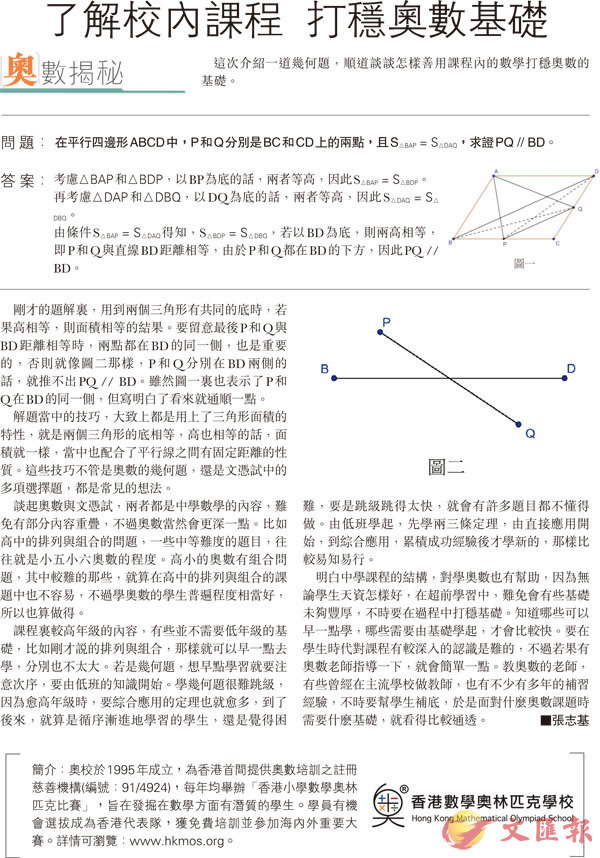
剛才的題解裏,用到兩個三角形有共同的底時,若果高相等,則面積相等的結果。要留意最後P和Q與BD距離相等時,兩點都在BD的同一側,也是重要的,否則就像圖二那樣,P和Q分別在BD兩側的話,就推不出PQ // BD。雖然圖一裏也表示了P和Q在BD的同一側,但寫明白了看來就通順一點。
解題當中的技巧,大致上都是用上了三角形面積的特性,就是兩個三角形的底相等,高也相等的話,面積就一樣,當中也配合了平行線之間有固定距離的性質。這些技巧不管是奧數的幾何題,還是文憑試中的多項選擇題,都是常見的想法。
談起奧數與文憑試,兩者都是中學數學的內容,難免有部分內容重疊,不過奧數當然會更深一點。比如高中的排列與組合的問題,一些中等難度的題目,往往就是小五小六奧數的程度。高小的奧數有組合問題,其中較難的那些,就算在高中的排列與組合的課題中也不容易,不過學奧數的學生普遍程度相當好,所以也算做得。
課程裏較高年級的內容,有些並不需要低年級的基礎,比如剛才說的排列與組合,那樣就可以早一點去學,分別也不太大。若是幾何題,想早點學習就要注意次序,要由低班的知識開始。學幾何題很難跳級,因為愈高年級時,要綜合應用的定理也就愈多,到了後來,就算是循序漸進地學習的學生,還是覺得困難,要是跳級跳得太快,就會有許多題目都不懂得做。由低班學起,先學兩三條定理,由直接應用開始,到綜合應用,累積成功經驗後才學新的,那樣比較易知易行。
明白中學課程的結構,對學奧數也有幫助,因為無論學生天資怎樣好,在超前學習中,難免會有些基礎未夠豐厚,不時要在過程中打穩基礎。知道哪些可以早一點學,哪些需要由基礎學起,才會比較快。要在學生時代對課程有較深入的認識是難的,不過若果有奧數老師指導一下,就會簡單一點。教奧數的老師,有些曾經在主流學校做教師,也有不少有多年的補習經驗,不時要幫學生補底,於是面對什麼奧數課題時需要什麽基礎,就看得比較通透。 ■張志基
簡介:奧校於1995年成立,為香港首間提供奧數培訓之註冊慈善機構(編號:91/4924),每年均舉辦「香港小學數學奧林匹克比賽」,旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊,獲免費培訓並參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
■香港數學奧林匹克學校

