小學時學倍數的概念,久不久會問起一些類似「100或以內有多少個3的倍數」的問題。答案也不複雜,就是100÷3=33...1,有33個3的倍數。或者改改數字,問一問「100以內又有多少個4的倍數」,那也很容易,就是100÷4=25,有25個4的倍數。
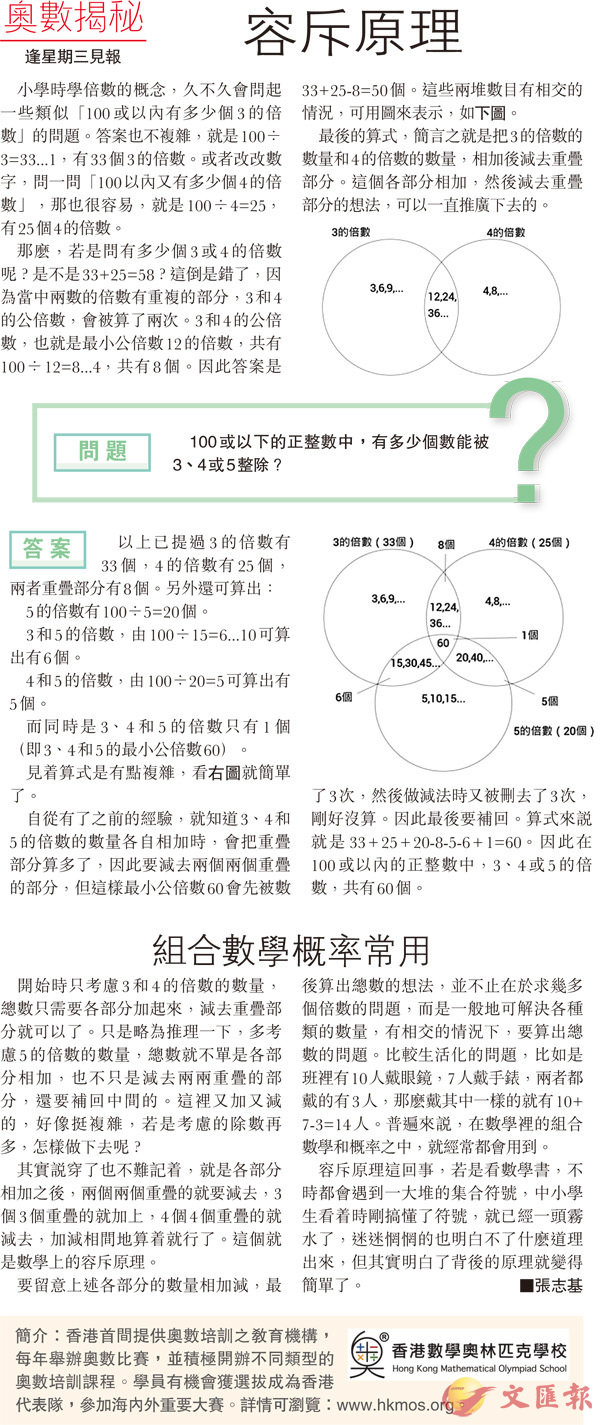
那麽,若是問有多少個3或4的倍數呢?是不是33+25=58?這倒是錯了,因為當中兩數的倍數有重複的部分,3和4的公倍數,會被算了兩次。3和4的公倍數,也就是最小公倍數12的倍數,共有100÷12=8...4,共有8個。因此答案是33+25-8=50個。這些兩堆數目有相交的情況,可用圖來表示,如下圖。
最後的算式,簡言之就是把3的倍數的數量和4的倍數的數量,相加後減去重疊部分。這個各部分相加,然後減去重疊部分的想法,可以一直推廣下去的。
問 題
100或以下的正整數中,有多少個數能被3、4或5整除?
答 案
以上已提過3的倍數有33個,4的倍數有25個,兩者重疊部分有8個。另外還可算出:
5的倍數有100÷5=20個。
3和5的倍數,由100÷15=6...10可算出有6個。
4和5的倍數,由100÷20=5可算出有5個。
而同時是3、4和5的倍數只有1個(即3、4和5的最小公倍數60)。
見着算式是有點複雜,看右圖就簡單了。
自從有了之前的經驗,就知道3、4和5的倍數的數量各自相加時,會把重疊部分算多了,因此要減去兩個兩個重疊的部分,但這樣最小公倍數60會先被數了3次,然後做減法時又被刪去了3次,剛好沒算。因此最後要補回。算式來說就是33+25+20-8-5-6+1=60。因此在100或以內的正整數中,3、4或5的倍數,共有60個。
組合數學概率常用
開始時只考慮3和4的倍數的數量,總數只需要各部分加起來,減去重疊部分就可以了。只是略為推理一下,多考慮5的倍數的數量,總數就不單是各部分相加,也不只是減去兩兩重疊的部分,還要補回中間的。這裡又加又減的,好像挺複雜,若是考慮的除數再多,怎樣做下去呢?
其實說穿了也不難記着,就是各部分相加之後,兩個兩個重疊的就要減去,3個3個重疊的就加上,4個4個重疊的就減去,加減相間地算着就行了。這個就是數學上的容斥原理。
要留意上述各部分的數量相加減,最後算出總數的想法,並不止在於求幾多個倍數的問題,而是一般地可解決各種類的數量,有相交的情況下,要算出總數的問題。比較生活化的問題,比如是班裡有10人戴眼鏡,7人戴手錶,兩者都戴的有3人,那麽戴其中一樣的就有10+7-3=14人。普遍來說,在數學裡的組合數學和概率之中,就經常都會用到。
容斥原理這回事,若是看數學書,不時都會遇到一大堆的集合符號,中小學生看着時剛搞懂了符號,就已經一頭霧水了,迷迷惘惘的也明白不了什麽道理出來,但其實明白了背後的原理就變得簡單了。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

