奧數除了是一些較難的題目,有時也會有一些特別的解難技巧,令到一些問題可以有另一角度的理解。以下分享的這一道題目,若是有中四或以上關於三角函數的知識,是很容易解決的。不過這裡嘗試用構造圖形的方法,去了解這個結果。
問 題
設0o<θ<90o,求證:1<sinθ+cosθ⩽ [2]。
答 案
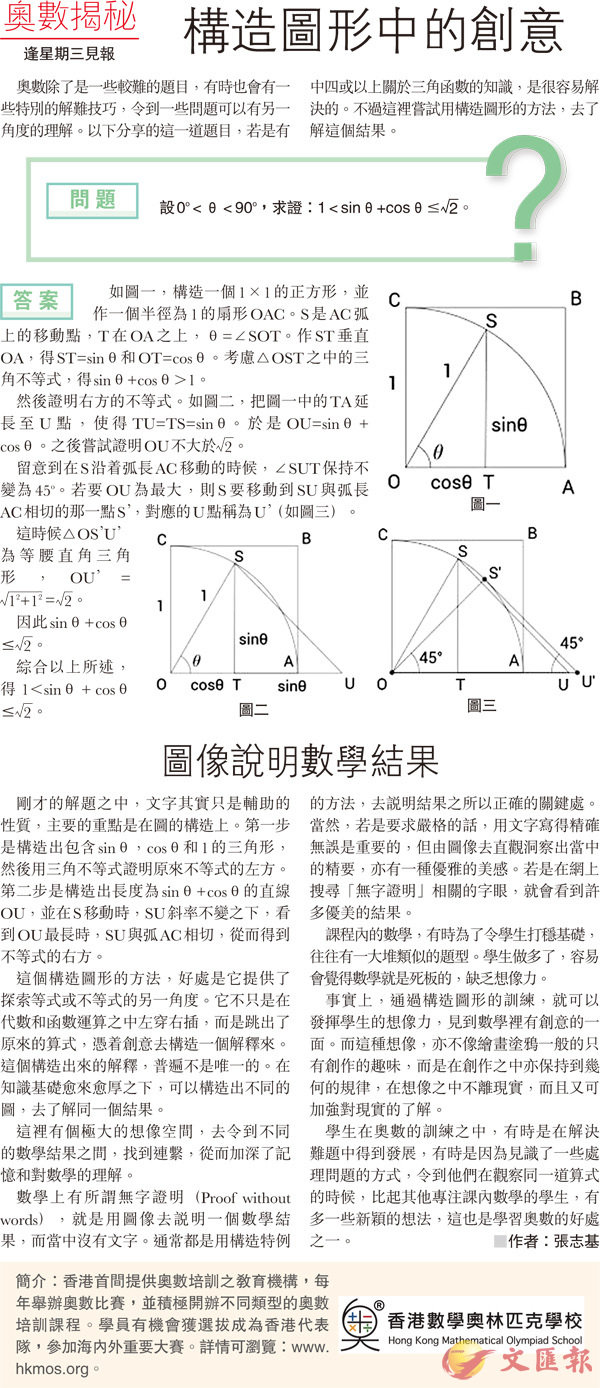
如圖一,構造一個1×1的正方形,並作一個半徑為1的扇形OAC。S是AC弧上的移動點,T在OA之上,θ=∠SOT。作ST垂直OA,得ST=sinθ和OT=cosθ。考慮△OST之中的三角不等式,得sinθ+cosθ>1。
然後證明右方的不等式。如圖二,把圖一中的TA延長至U點,使得TU=TS=sinθ。於是OU=sinθ+cosθ。之後嘗試證明OU不大於 [2]。
留意到在S沿着弧長AC移動的時候,∠SUT保持不變為45o。若要OU為最大,則S要移動到SU與弧長AC相切的那一點S’,對應的U點稱為U’(如圖三)。
這時候△OS’U’為等腰直角三角形,OU’= [12+12][=] [2]。
因此sinθ+cosθ⩽ [2]。
綜合以上所述,得1<sinθ+cosθ⩽ [2]。
圖像說明數學結果
剛才的解題之中,文字其實只是輔助的性質,主要的重點是在圖的構造上。第一步是構造出包含sinθ,cosθ和1的三角形,然後用三角不等式證明原來不等式的左方。第二步是構造出長度為sinθ+cosθ的直線OU,並在S移動時,SU斜率不變之下,看到OU最長時,SU與弧AC相切,從而得到不等式的右方。
這個構造圖形的方法,好處是它提供了探索等式或不等式的另一角度。它不只是在代數和函數運算之中左穿右插,而是跳出了原來的算式,憑着創意去構造一個解釋來。這個構造出來的解釋,普遍不是唯一的。在知識基礎愈來愈厚之下,可以構造出不同的圖,去了解同一個結果。
這裡有個極大的想像空間,去令到不同的數學結果之間,找到連繫,從而加深了記憶和對數學的理解。
數學上有所謂無字證明(Proof without words),就是用圖像去說明一個數學結果,而當中沒有文字。通常都是用構造特例的方法,去說明結果之所以正確的關鍵處。當然,若是要求嚴格的話,用文字寫得精確無誤是重要的,但由圖像去直觀洞察出當中的精要,亦有一種優雅的美感。若是在網上搜尋「無字證明」相關的字眼,就會看到許多優美的結果。
課程內的數學,有時為了令學生打穩基礎,往往有一大堆類似的題型。學生做多了,容易會覺得數學就是死板的,缺乏想像力。
事實上,通過構造圖形的訓練,就可以發揮學生的想像力,見到數學裡有創意的一面。而這種想像,亦不像繪畫塗鴉一般的只有創作的趣味,而是在創作之中亦保持到幾何的規律,在想像之中不離現實,而且又可加強對現實的了解。
學生在奧數的訓練之中,有時是在解決難題中得到發展,有時是因為見識了一些處理問題的方式,令到他們在觀察同一道算式的時候,比起其他專注課內數學的學生,有多一些新穎的想法,這也是學習奧數的好處之一。 ■作者:張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

