三角形經常出現在幾何題目中,而內角的角平分線,也是經常會添加的線段,有時會用作輔助線。關於角平分線,有一道相關定理,稱為角平分線定理,這在課程內沒有特別提及,即使出現,多數也只是其中一道習題。不過用起來挺好用,值得談談。
在介紹定理前,先分享一道相關題目。
問 題
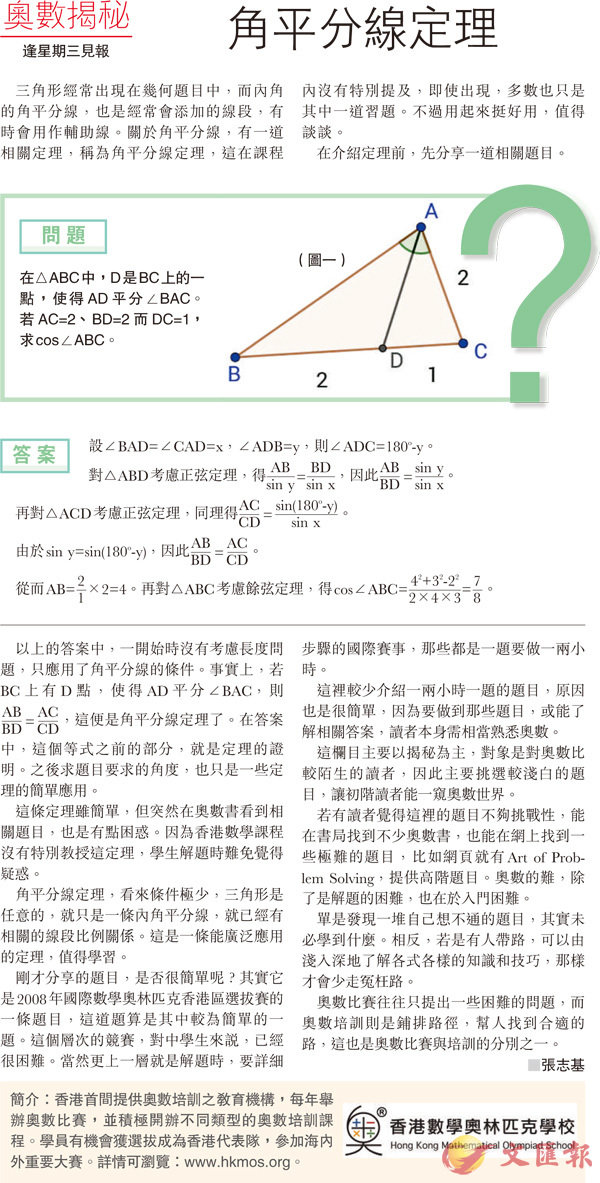
在△ABC中,D是BC上的一點,使得AD平分∠BAC。若AC=2、BD=2而DC=1,求cos∠ABC。
答 案
設∠BAD=∠CAD=x,∠ADB=y,則∠ADC=180o-y。
對△ABD考慮正弦定理,得[AB][sin y] [BD][sin x] [=],因此[AB][sin y] [BD][sin x] [=]。
再對△ACD考慮正弦定理,同理得[AC][sin(180o-y)] [CD][sin x] [=]。
由於sin y=sin(180o-y),因此[AB] [BD][=][AC] [CD]。
從而AB=[2] [1]×2=4。再對△ABC考慮餘弦定理,得cos∠ABC=[42+32-22] [2×4×3]=[7] [8]。
以上的答案中,一開始時沒有考慮長度問題,只應用了角平分線的條件。事實上,若BC上有D點,使得AD平分∠BAC,則[AB] [BD][=][AC] [CD],這便是角平分線定理了。在答案中,這個等式之前的部分,就是定理的證明。之後求題目要求的角度,也只是一些定理的簡單應用。
這條定理雖簡單,但突然在奧數書看到相關題目,也是有點困惑。因為香港數學課程沒有特別教授這定理,學生解題時難免覺得疑惑。
角平分線定理,看來條件極少,三角形是任意的,就只是一條內角平分線,就已經有相關的線段比例關係。這是一條能廣泛應用的定理,值得學習。
剛才分享的題目,是否很簡單呢?其實它是2008年國際數學奧林匹克香港區選拔賽的一條題目,這道題算是其中較為簡單的一題。這個層次的競賽,對中學生來說,已經很困難。當然更上一層就是解題時,要詳細步驟的國際賽事,那些都是一題要做一兩小時。
這裡較少介紹一兩小時一題的題目,原因也是很簡單,因為要做到那些題目,或能了解相關答案,讀者本身需相當熟悉奧數。
這欄目主要以揭秘為主,對象是對奧數比較陌生的讀者,因此主要挑選較淺白的題目,讓初階讀者能一窺奧數世界。
若有讀者覺得這裡的題目不夠挑戰性,能在書局找到不少奧數書,也能在網上找到一些極難的題目,比如網頁就有Art of Problem Solving,提供高階題目。奧數的難,除了是解題的困難,也在於入門困難。
單是發現一堆自己想不通的題目,其實未必學到什麼。相反,若是有人帶路,可以由淺入深地了解各式各樣的知識和技巧,那樣才會少走冤枉路。
奧數比賽往往只提出一些困難的問題,而奧數培訓則是鋪排路徑,幫人找到合適的路,這也是奧數比賽與培訓的分別之一。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

