小時候做手工,不時都會用大大小小七彩繽紛的正方形紙,剪出一個又一個的圖案,去裝飾着自己的小作品,好像聖誕卡和小燈籠之類的。
原來在剪紙的過程中,也有些數學隱藏在裡面。
問 題 一
證明任意兩張邊長不相等的正方形咭紙,都可以剪開其中一部分之後,重新拼成一個大正方形。
答 案
設較大的正方形邊長為a,較小的正方形邊長為b。
若是能夠重新拼成一個大正方形,那麽它的面積必然是a2+b2。因此它的邊長必然是[a2+b2] 。這個算式不難聯想到畢氏定理,[a2+b2] 看來是一個直角三角形的斜邊,而該直角三角形的直角邊分別為a和b。
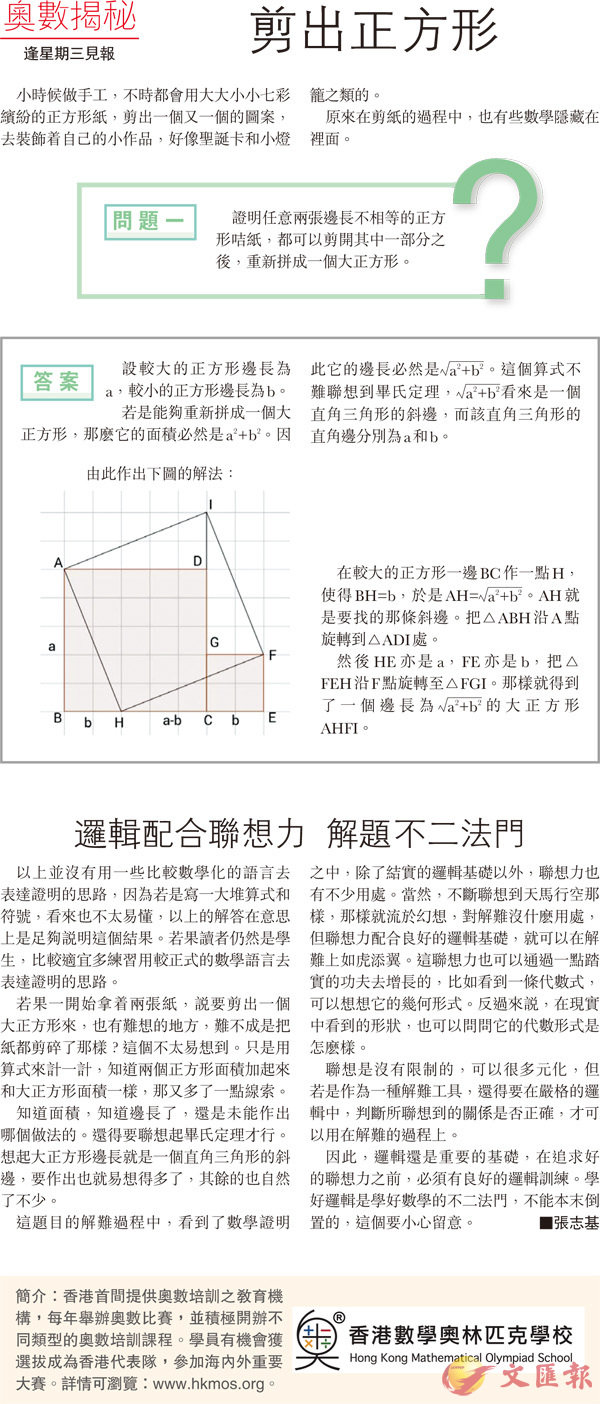
由此作出下圖的解法:
在較大的正方形一邊BC作一點H,使得BH=b,於是AH=[a2+b2] 。AH就是要找的那條斜邊。把△ABH沿A點旋轉到△ADI處。
然後HE亦是a,FE亦是b,把△FEH沿F點旋轉至△FGI。那樣就得到了一個邊長為[a2+b2] 的大正方形AHFI。
邏輯配合聯想力 解題不二法門
以上並沒有用一些比較數學化的語言去表達證明的思路,因為若是寫一大堆算式和符號,看來也不太易懂,以上的解答在意思上是足夠說明這個結果。若果讀者仍然是學生,比較適宜多練習用較正式的數學語言去表達證明的思路。
若果一開始拿着兩張紙,說要剪出一個大正方形來,也有難想的地方,難不成是把紙都剪碎了那樣?這個不太易想到。只是用算式來計一計,知道兩個正方形面積加起來和大正方形面積一樣,那又多了一點線索。
知道面積,知道邊長了,還是未能作出哪個做法的。還得要聯想起畢氏定理才行。想起大正方形邊長就是一個直角三角形的斜邊,要作出也就易想得多了,其餘的也自然了不少。
這題目的解難過程中,看到了數學證明之中,除了結實的邏輯基礎以外,聯想力也有不少用處。當然,不斷聯想到天馬行空那樣,那樣就流於幻想,對解難沒什麽用處,但聯想力配合良好的邏輯基礎,就可以在解難上如虎添翼。這聯想力也可以通過一點踏實的功夫去增長的,比如看到一條代數式,可以想想它的幾何形式。反過來說,在現實中看到的形狀,也可以問問它的代數形式是怎麽樣。
聯想是沒有限制的,可以很多元化,但若是作為一種解難工具,還得要在嚴格的邏輯中,判斷所聯想到的關係是否正確,才可以用在解難的過程上。
因此,邏輯還是重要的基礎,在追求好的聯想力之前,必須有良好的邏輯訓練。學好邏輯是學好數學的不二法門,不能本末倒置的,這個要小心留意。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

