幾何的問題中,有時不同的線段和角度之間,也會有些加減乘除的運算,來描述不同數量的關係。若是線段都是連接着的,那倒是容易一點。相反,若是兩條線段之間看來沒什麽關係的,或者是距離很遠,加起來怎樣,比較難有什麽了解,更難去掌握它們與其他資料運算起來有什麽關係。
以下分享一道幾何問題,談談箇中連接線段的技巧。
問 題
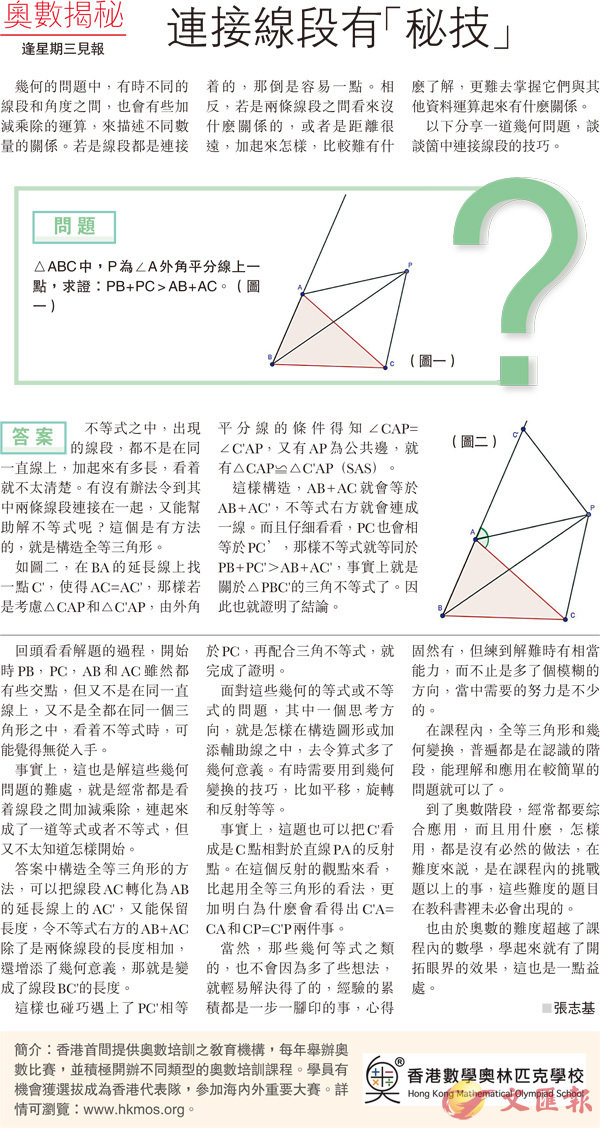
△ABC中,P為∠A外角平分線上一點,求證:PB+PC>AB+AC。(圖一)
答 案
不等式之中,出現的線段,都不是在同一直線上,加起來有多長,看着就不太清楚。有沒有辦法令到其中兩條線段連接在一起,又能幫助解不等式呢?這個是有方法的,就是構造全等三角形。
如圖二,在BA的延長線上找一點C',使得AC=AC',那樣若是考慮△CAP和△C'AP,由外角平分線的條件得知∠CAP=∠C'AP,又有AP為公共邊,就有△CAP?△C'AP(SAS)。
這樣構造,AB+AC就會等於AB+AC',不等式右方就會連成一線。而且仔細看看,PC也會相等於PC',那樣不等式就等同於PB+PC'>AB+AC',事實上就是關於△PBC'的三角不等式了。因此也就證明了結論。
回頭看看解題的過程,開始時PB,PC,AB和AC雖然都有些交點,但又不是在同一直線上,又不是全都在同一個三角形之中,看着不等式時,可能覺得無從入手。
事實上,這也是解這些幾何問題的難處,就是經常都是看着線段之間加減乘除,連起來成了一道等式或者不等式,但又不太知道怎樣開始。
答案中構造全等三角形的方法,可以把線段AC轉化為AB的延長線上的AC',又能保留長度,令不等式右方的AB+AC除了是兩條線段的長度相加,還增添了幾何意義,那就是變成了線段BC'的長度。
這樣也碰巧遇上了PC'相等於PC,再配合三角不等式,就完成了證明。
面對這些幾何的等式或不等式的問題,其中一個思考方向,就是怎樣在構造圖形或加添輔助線之中,去令算式多了幾何意義。有時需要用到幾何變換的技巧,比如平移,旋轉和反射等等。
事實上,這題也可以把C'看成是C點相對於直線PA的反射點。在這個反射的觀點來看,比起用全等三角形的看法,更加明白為什麽會看得出C'A=CA和CP=C'P兩件事。
當然,那些幾何等式之類的,也不會因為多了些想法,就輕易解決得了的,經驗的累積都是一步一腳印的事,心得固然有,但練到解難時有相當能力,而不止是多了個模糊的方向,當中需要的努力是不少的。
在課程內,全等三角形和幾何變換,普遍都是在認識的階段,能理解和應用在較簡單的問題就可以了。
到了奧數階段,經常都要綜合應用,而且用什麽,怎樣用,都是沒有必然的做法,在難度來說,是在課程內的挑戰題以上的事,這些難度的題目在教科書裡未必會出現的。
也由於奧數的難度超越了課程內的數學,學起來就有了開拓眼界的效果,這也是一點益處。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

