上回提到小英如何運用逆向思考來找出「拿石子遊戲」的必勝策略(winning strategy)(詳見6月22日香港文匯報A28版)。經過若干個回合後,小明看穿了小英的策略,於是他建議新的遊戲規則:
1. 把60顆石子排成一個任意的矩形,由一人決定形狀,另一人則先拿石子。
2. 兩人輪流拿取石子,數目不限,但必須最少1顆;位置也不限,但必須在同一橫行或同一直行。
3. 拿到最後一顆石子的便是勝利者。
規則變仍必勝?
遊戲開始,由小英負責把石子排成一個5×12的矩形,而小明則先拿石子。遊戲規則改變了,究竟是否依然先拿石子的必勝?是否每行留下相同數量的石子依然是必勝策略?
於是小英運用逆向思考,想想遊戲終結前的可能情況。
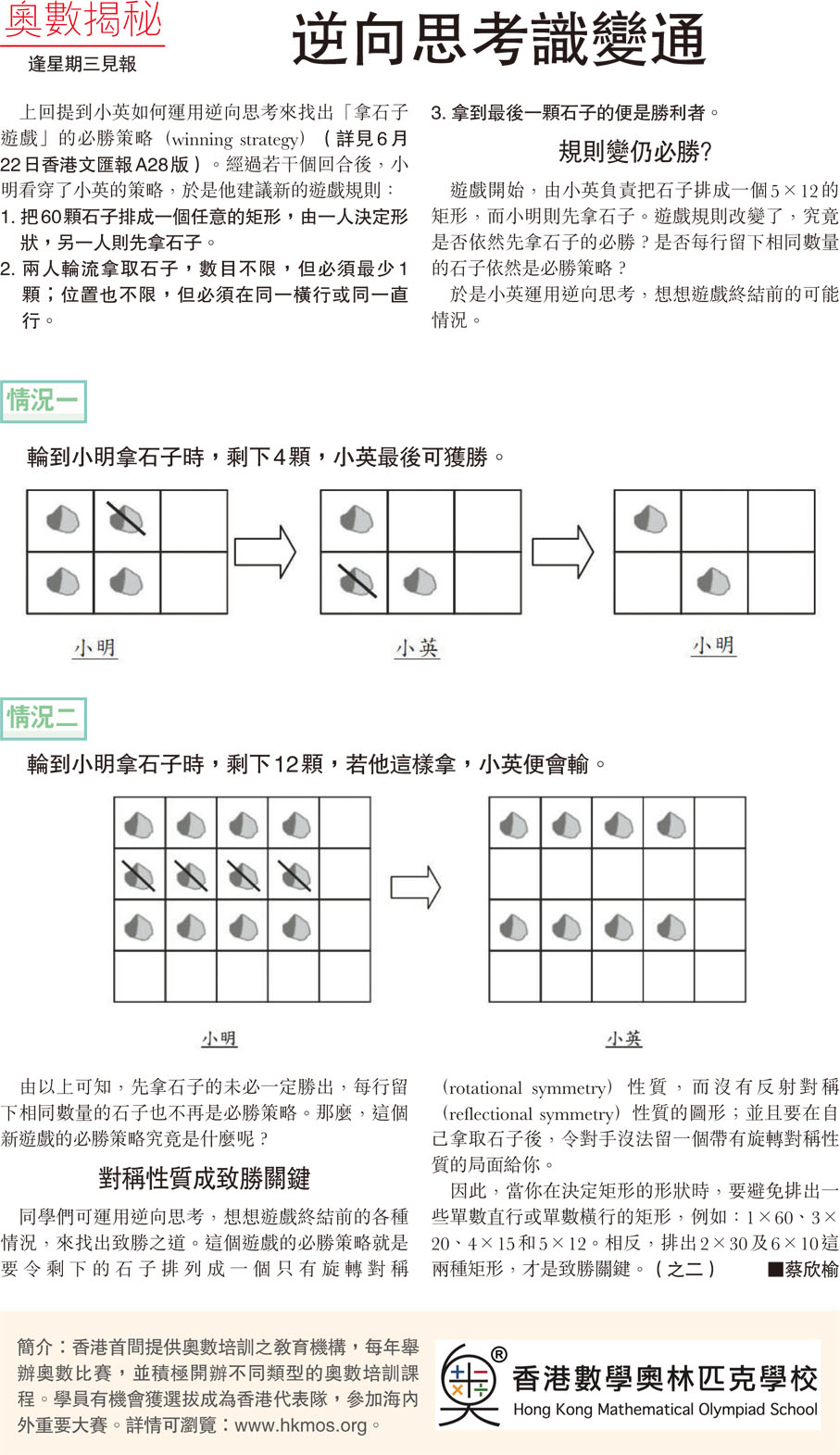
情況一:輪到小明拿石子時,剩下4顆,小英最後可獲勝。
情況二:輪到小明拿石子時,剩下12顆,若他這樣拿,小英便會輸。
由以上可知,先拿石子的未必一定勝出,每行留下相同數量的石子也不再是必勝策略。那麼,這個新遊戲的必勝策略究竟是什麼呢?
對稱性質成致勝關鍵
同學們可運用逆向思考,想想遊戲終結前的各種情況,來找出致勝之道。這個遊戲的必勝策略就是要令剩下的石子排列成一個只有旋轉對稱(rotational symmetry)性質,而沒有反射對稱(reflectional symmetry)性質的圖形;並且要在自己拿取石子後,令對手沒法留一個帶有旋轉對稱性質的局面給你。
因此,當你在決定矩形的形狀時,要避免排出一些單數直行或單數橫行的矩形,例如:1×60、3×20、4×15和5×12。相反,排出2×30及6×10這兩種矩形,才是致勝關鍵。(之二) ■蔡欣榆
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報
