天氣炎熱的日子,有時會去便利店買支甜筒,拿着甜筒,從側邊看看,那是一個等腰三角形。或者買個飯糰,正面看看,也是一個三角形。原來平面的三角形,許多時候都是一些立體圖形的某一面,比如錐體。可以說,三角形滲透在生活的每個角落中。究竟三角學在現實生活的實際應用是什麼?讓我們透過以下兩個例子:如何找出一幢大廈的高度和如何計算兩艘輪船之間的距離,來了解一下。
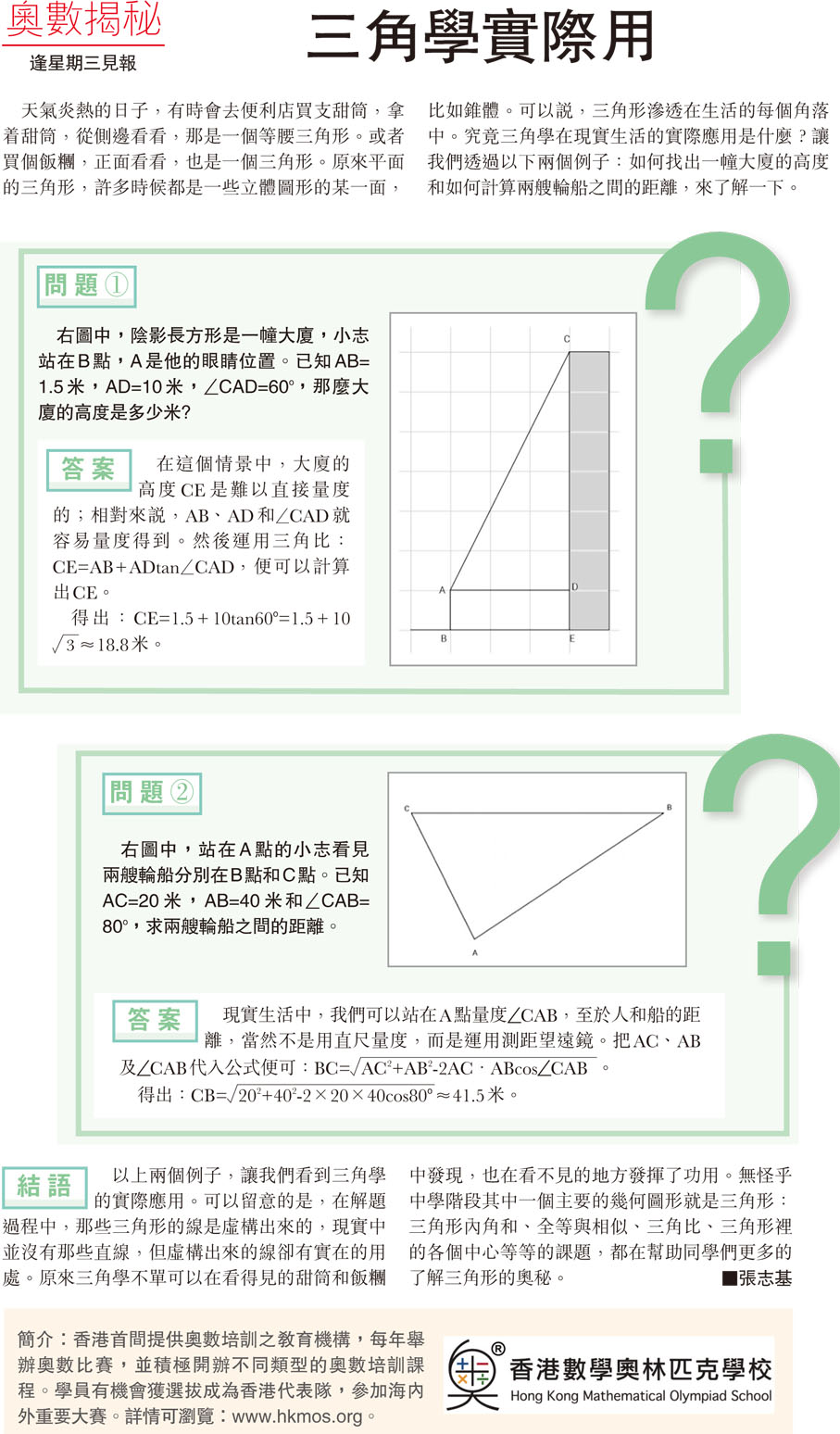
右圖中,陰影長方形是一幢大廈,小志站在B點,A是他的眼睛位置。已知AB=1.5米,AD=10米, CAD=60o,那麼大廈的高度是多少米?
問 題 ①
答 案
在這個情景中,大廈的高度CE是難以直接量度的;相對來說,AB、AD和 CAD就容易量度得到。然後運用三角比:CE=AB+ADtan CAD,便可以計算出CE。
得出:CE=1.5+10tan60o=1.5+10 [3]?18.8米。
問 題 ②
右圖中,站在A點的小志看見兩艘輪船分別在B點和C點。已知AC=20米,AB=40米和 CAB=80o,求兩艘輪船之間的距離。
答案
現實生活中,我們可以站在A點量度 CAB,至於人和船的距離,當然不是用直尺量度,而是運用測距望遠鏡。把AC、AB及 CAB代入公式便可:BC=[AC2+AB2-2AC.ABcos CAB] 。
得出:CB=[202+402-2×20×40cos80o] ?41.5米。
結 語
以上兩個例子,讓我們看到三角學的實際應用。可以留意的是,在解題過程中,那些三角形的線是虛構出來的,現實中並沒有那些直線,但虛構出來的線卻有實在的用處。原來三角學不單可以在看得見的甜筒和飯糰中發現,也在看不見的地方發揮了功用。無怪乎中學階段其中一個主要的幾何圖形就是三角形:三角形內角和、全等與相似、三角比、三角形裡的各個中心等等的課題,都在幫助同學們更多的了解三角形的奧秘。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報
