寒冷的冬天裡,穿上大衣走到室內,一時間覺得暖得來,還真有點焗,頭腦昏昏的,又不想開窗令寒風入來,就打開風扇。看着扇葉轉着轉着,由初時的3片葉,漸漸變成了圓圓的一圈,在扇葉上一口一口的小螺絲,在旋轉中的軌跡,成為了一個一個圓形。
為什麽是圓形呢?就是因為在旋轉的過程中,移動點和旋轉的中心保持相等的距離。旋轉作為一種幾何變換,在初中的數學課程內也有提到的,常見的問題之一就是怎樣在知道一個在坐標上的長方形以原點為中心順時針旋轉90o後,新的圖像在什麽位置。或者是再數學化一點,就是坐標上的點P(2,1),以(0,0)為中心,順時針旋轉90o後,新的點P'是什麽位置,那就是(1,-2)。
旋轉前後的點(2,1)和(1,-2),與原點的距離都一樣。就長方形的情況來說,每條邊旋轉後都是順時針轉了90o。普遍來說,就是一個圖形以一點旋轉θo,則圖形上每條直線在旋轉後都轉了θo。
這些小小的結果可以有什麽應用呢?看看以下的問題。
問 題
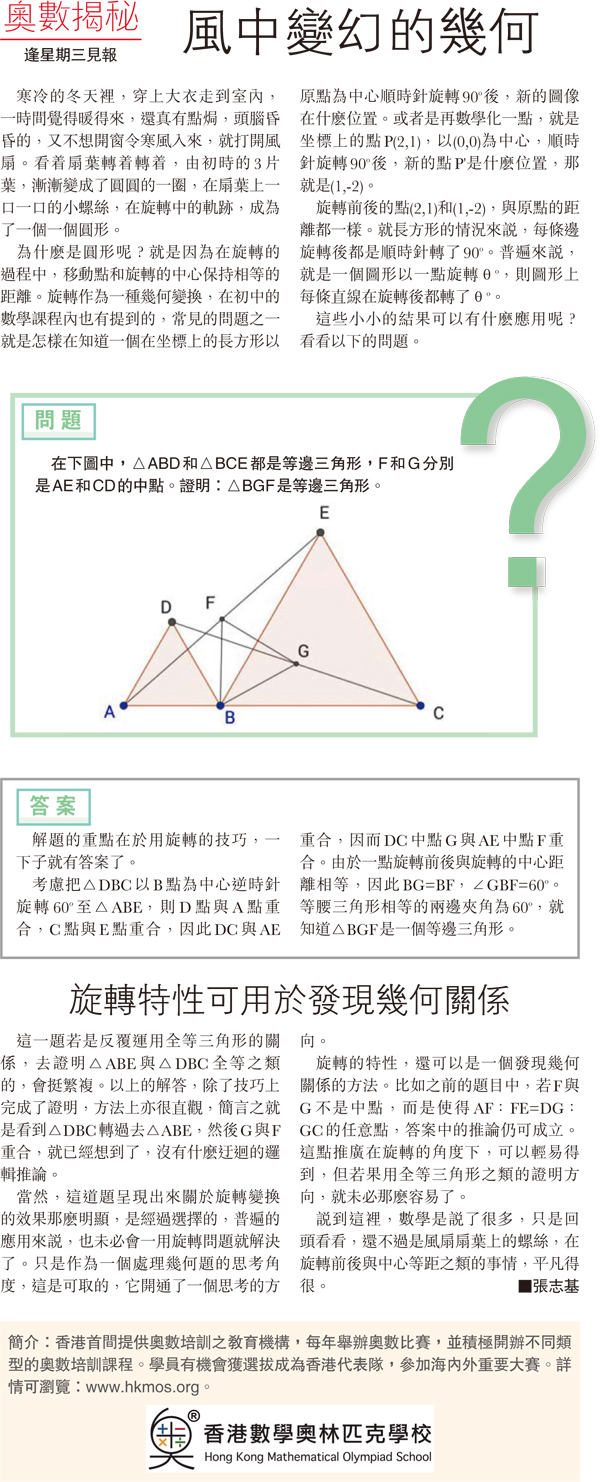
在下圖中,△ABD和△BCE都是等邊三角形,F和G分別是AE和CD的中點。證明:△BGF是等邊三角形。
答 案
解題的重點在於用旋轉的技巧,一下子就有答案了。
考慮把△DBC以B點為中心逆時針旋轉60o至△ABE,則D點與A點重合,C點與E點重合,因此DC與AE重合,因而DC中點G與AE中點F重合。由於一點旋轉前後與旋轉的中心距離相等,因此BG=BF,∠GBF=60o。等腰三角形相等的兩邊夾角為60o,就知道△BGF是一個等邊三角形。
旋轉特性可用於發現幾何關係
這一題若是反覆運用全等三角形的關係,去證明△ABE與△DBC全等之類的,會挺繁複。以上的解答,除了技巧上完成了證明,方法上亦很直觀,簡言之就是看到△DBC轉過去△ABE,然後G與F重合,就已經想到了,沒有什麽迂迴的邏輯推論。
當然,這道題呈現出來關於旋轉變換的效果那麽明顯,是經過選擇的,普遍的應用來說,也未必會一用旋轉問題就解決了。只是作為一個處理幾何題的思考角度,這是可取的,它開通了一個思考的方向。
旋轉的特性,還可以是一個發現幾何關係的方法。比如之前的題目中,若F與G不是中點,而是使得AF:FE=DG:GC的任意點,答案中的推論仍可成立。這點推廣在旋轉的角度下,可以輕易得到,但若果用全等三角形之類的證明方向,就未必那麽容易了。
說到這裡,數學是說了很多,只是回頭看看,還不過是風扇扇葉上的螺絲,在旋轉前後與中心等距之類的事情,平凡得很。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

