平日走在街上,不時都會看到許多高高懸掛着的廣告牌,有些挺漂亮的,也會想仔細看清楚一點。距離遠的時候,固然看不清,太近了,比如在廣告牌下方,也會看不清的,因此能不能看清楚,也不只是距離遠近的問題。這當中有個最佳位置。
問 題
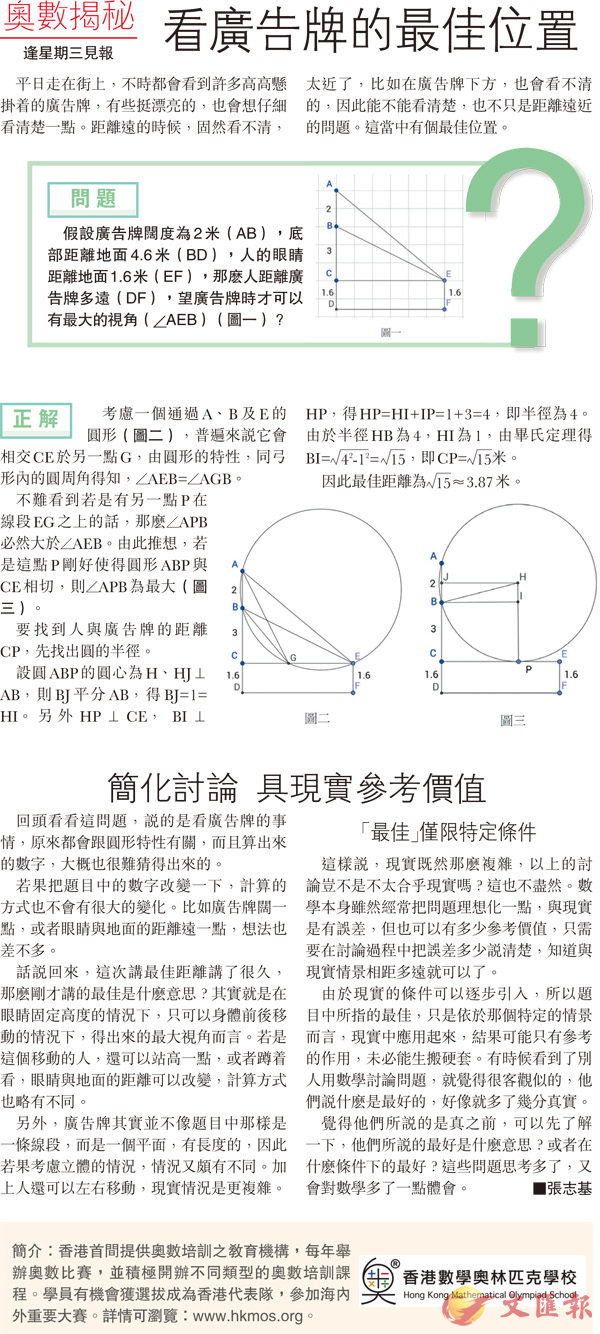
假設廣告牌闊度為2米(AB),底部距離地面4.6米(BD),人的眼睛距離地面1.6米(EF),那麽人距離廣告牌多遠(DF),望廣告牌時才可以有最大的視角( AEB)(圖一)?
正 解
考慮一個通過A、B及E的圓形(圖二),普遍來說它會相交CE於另一點G,由圓形的特性,同弓形內的圓周角得知, AEB= AGB。
不難看到若是有另一點P在線段EG之上的話,那麽 APB必然大於 AEB。由此推想,若是這點P剛好使得圓形ABP與CE相切,則 APB為最大(圖三)。
要找到人與廣告牌的距離CP,先找出圓的半徑。
設圓ABP的圓心為H、HJ⊥AB,則BJ平分AB,得BJ=1=HI。另外HP⊥CE, BI⊥HP,得HP=HI+IP=1+3=4,即半徑為4。由於半徑HB為4,HI為1,由畢氏定理得BI=[42-12= 15] ,即CP=[15] 米。
因此最佳距離為[15] ?3.87米。
簡化討論 具現實參考價值
回頭看看這問題,說的是看廣告牌的事情,原來都會跟圓形特性有關,而且算出來的數字,大概也很難猜得出來的。
若果把題目中的數字改變一下,計算的方式也不會有很大的變化。比如廣告牌闊一點,或者眼睛與地面的距離遠一點,想法也差不多。
話說回來,這次講最佳距離講了很久,那麽剛才講的最佳是什麽意思?其實就是在眼睛固定高度的情況下,只可以身體前後移動的情況下,得出來的最大視角而言。若是這個移動的人,還可以站高一點,或者蹲着看,眼睛與地面的距離可以改變,計算方式也略有不同。
另外,廣告牌其實並不像題目中那樣是一條線段,而是一個平面,有長度的,因此若果考慮立體的情況,情況又頗有不同。加上人還可以左右移動,現實情況是更複雜。
「最佳」僅限特定條件
這樣說,現實既然那麽複雜,以上的討論豈不是不太合乎現實嗎?這也不盡然。數學本身雖然經常把問題理想化一點,與現實是有誤差,但也可以有多少參考價值,只需要在討論過程中把誤差多少說清楚,知道與現實情景相距多遠就可以了。
由於現實的條件可以逐步引入,所以題目中所指的最佳,只是依於那個特定的情景而言,現實中應用起來,結果可能只有參考的作用,未必能生搬硬套。有時候看到了別人用數學討論問題,就覺得很客觀似的,他們說什麽是最好的,好像就多了幾分真實。
覺得他們所說的是真之前,可以先了解一下,他們所說的最好是什麽意思?或者在什麽條件下的最好?這些問題思考多了,又會對數學多了一點體會。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

