奧數在學習的過程中,會發現有些知識並不止是一些數學上的技巧,亦不算是一些理論或者公式,而是一些思想方法。這個在課內比較少見,因為憑空說思想太抽象,總得要依着一些基礎。
然而,在課程內的數學,大部分時候,普遍學生能掌握基礎已經不錯,再提起思想方法之類的,有點困難。
解難之中有些思想方法是有用的,其中一個常用的就是極端原理。
問 題
在等邊三角形之中,任意取一點P,證明:由P到三邊的垂直距離之和為固定數值。
答 案
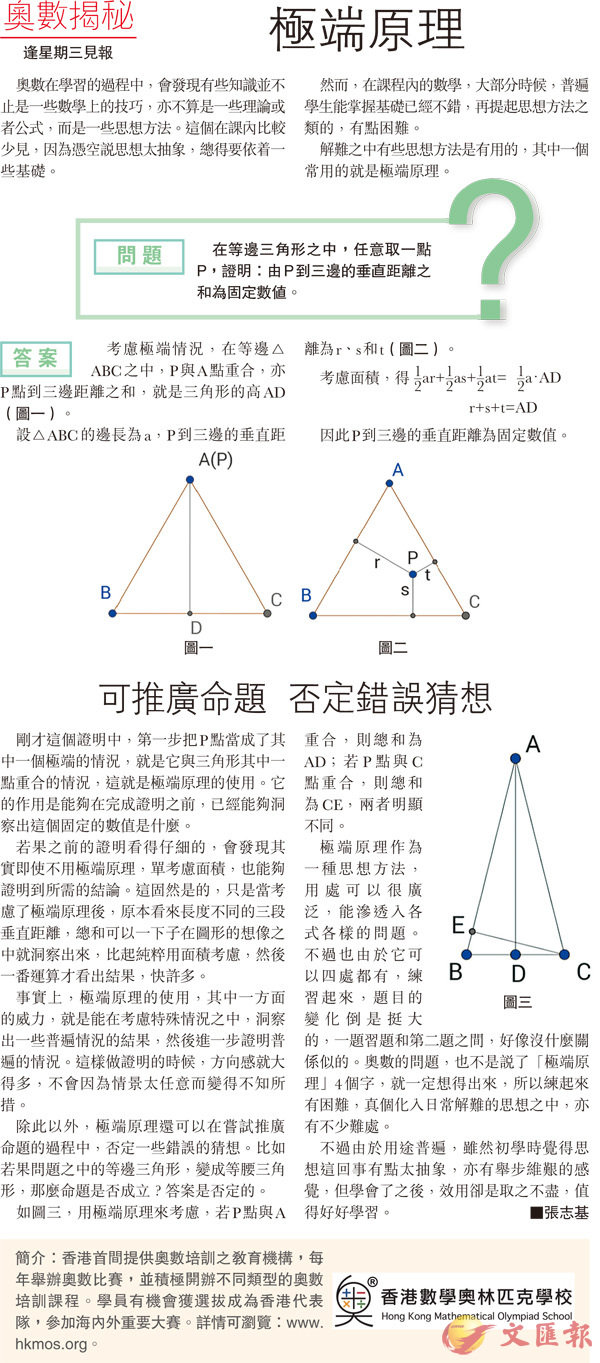
考慮極端情況,在等邊△ABC之中,P與A點重合,亦P點到三邊距離之和,就是三角形的高AD(圖一)。
設△ABC的邊長為a,P到三邊的垂直距離為r、s和t(圖二)。
考慮面積,得 [2] [1][ar+][2] [1][as+][2] [1][at=][2] [1][a.AD]
r+s+t=AD
因此P到三邊的垂直距離為固定數值。
可推廣命題 否定錯誤猜想
剛才這個證明中,第一步把P點當成了其中一個極端的情況,就是它與三角形其中一點重合的情況,這就是極端原理的使用。它的作用是能夠在完成證明之前,已經能夠洞察出這個固定的數值是什麼。
若果之前的證明看得仔細的,會發現其實即使不用極端原理,單考慮面積,也能夠證明到所需的結論。這固然是的,只是當考慮了極端原理後,原本看來長度不同的三段垂直距離,總和可以一下子在圖形的想像之中就洞察出來,比起純粹用面積考慮,然後一番運算才看出結果,快許多。
事實上,極端原理的使用,其中一方面的威力,就是能在考慮特殊情況之中,洞察出一些普遍情況的結果,然後進一步證明普遍的情況。這樣做證明的時候,方向感就大得多,不會因為情景太任意而變得不知所措。
除此以外,極端原理還可以在嘗試推廣命題的過程中,否定一些錯誤的猜想。比如若果問題之中的等邊三角形,變成等腰三角形,那麼命題是否成立?答案是否定的。
如圖三,用極端原理來考慮,若P點與A重合,則總和為AD;若P點與C點重合,則總和為CE,兩者明顯不同。
極端原理作為一種思想方法,用處可以很廣泛,能滲透入各式各樣的問題。不過也由於它可以四處都有,練習起來,題目的變化倒是挺大的,一題習題和第二題之間,好像沒什麼關係似的。奧數的問題,也不是說了「極端原理」4個字,就一定想得出來,所以練起來有困難,真個化入日常解難的思想之中,亦有不少難處。
不過由於用途普遍,雖然初學時覺得思想這回事有點太抽象,亦有舉步維艱的感覺,但學會了之後,效用卻是取之不盡,值得好好學習。 ■張志基
簡介:香港首間提供奧數培訓之教育機構,每年舉辦奧數比賽,並積極開辦不同類型的奧數培訓課程。學員有機會獲選拔成為香港代表隊,參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
逢星期三見報

